
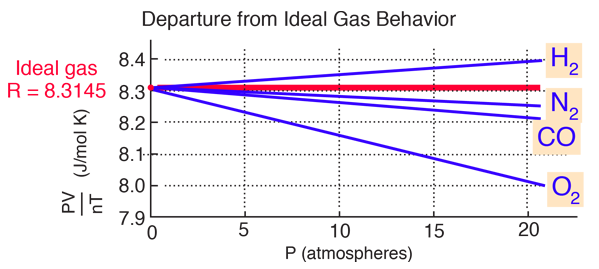
However, at high pressures, the molecules of a gas are crowded closer together, and the amount of empty space between the molecules is reduced. In general, real gases approximate this behavior at relatively low pressures and high temperatures. Particles of a hypothetical ideal gas have no significant volume and do not attract or repel each other. To determine why this is, consider the differences between real gas properties and what is expected of a hypothetical ideal gas. pressure shows that gases can exhibit significant deviations from the behavior predicted by the ideal gas law.Īs is apparent from Figure 8.35, the ideal gas law does not describe gas behavior well at relatively high pressures. This ratio is called the compressibility factor (Z) with:įigure 8.35 A graph of the compressibility factor (Z) vs. One way in which the accuracy of PV = nRT can be judged is by comparing the actual volume of 1 mole of gas (its molar volume, V m) to the molar volume of an ideal gas at the same temperature and pressure. In this section, the reasons for these deviations from ideal gas behavior are considered. As mentioned in the previous modules of this chapter, however, the behavior of a gas is often non-ideal, meaning that the observed relationships between its pressure, volume, and temperature are not accurately described by the gas laws. Thus far, the ideal gas law, PV = nRT, has been applied to a variety of different types of problems, ranging from reaction stoichiometry and empirical and molecular formula problems to determining the density and molar mass of a gas. Quantify non-ideal behavior by comparing computations of gas properties using the ideal gas law and the van der Waals equation.Define compressibility (Z) and describe how its variation with pressure reflects non-ideal behavior.Explain how these factors are represented in the van der Waals equation.Describe the physical factors that lead to deviations from ideal gas behavior.Selected values are provided in the table below.By the end of this section, you will be able to: When A=0, the activity coefficients are unity, thus describing an ideal mixture.Īn extensive range of recommended values for the Van Laar coefficients can be found in the literature. In this case the activity coefficients mirror at x 1=0.5.
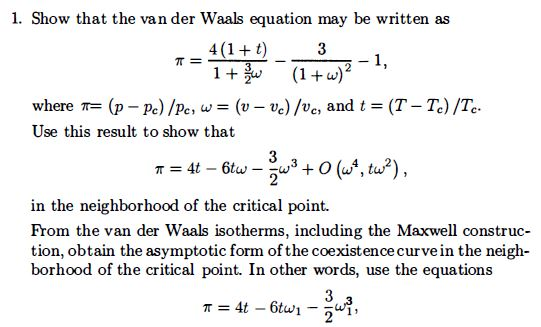
Van Laar derived the excess enthalpy from the van der Waals equation: H e x = b 1 X 1 b 2 X 2 b 1 X 1 + b 2 X 2 ( a 1 b 1 − a 2 b 2 ) 2 Because of this, the model lost the connection to molecular properties, and therefore it has to be regarded as an empirical model to correlate experimental results.

The original van der Waals parameters didn't give good description of vapor-liquid equilibria of phases, which forced the user to fit the parameters to experimental results.
The equation was derived from the Van der Waals equation. The Van Laar equation is a thermodynamic activity model, which was developed by Johannes van Laar in 1910-1913, to describe phase equilibria of liquid mixtures. Mathematical model of the thermodynamic activity of phase equilibria of liquid mixtures


 0 kommentar(er)
0 kommentar(er)
